
Probability and the new Advantage mechanic in D&D 5
There is a new mechanic in D&D 5 called advantage. As explained in the rules,
"When [advantage] happens, you roll a second d20 when you make the roll. Use the higher of the two rolls if you have advantage, and use the lower roll if you have disadvantage. For example, if you have disadvantage and roll a 17 and a 5, you use the 5. If you instead have advantage and roll those numbers, you use the 17." - Basic Rules v0.2 p. 57 and Player's Handbook p. 173
Without advantage the odds are simple: the chances of each number turning up on a d20 are 5%. The chance of rolling a natural 20 is 5%. The chance of suceeding at a DC 10 task is 55% (5% * 11 values on the die).
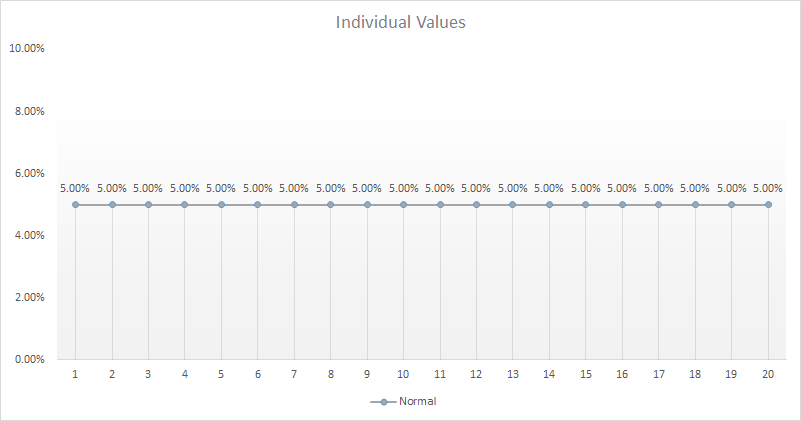
Here are the odds of rolling each number on a d20. It's a flat line; all twenty numbers are equally probable.
The new advantage mechanic tilts the scales of probability in your favor. Here are the odds of rolling a each number with advantage.
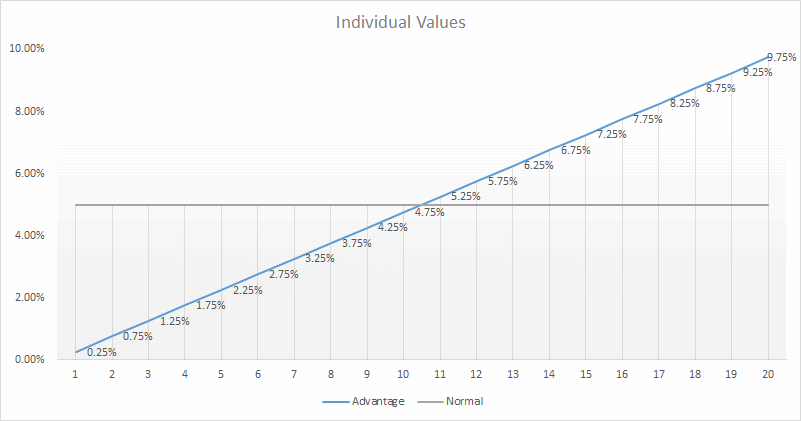
Now the odds have changed, and they've changed significantly at each end.
| Number to roll | Odds with Advantage | Normal Odds |
| Natural 1 | ¼% | 5% |
| Natural 20 | 9¾% | 5% |
With disadvantage the change is exactly the same but in the opposite direction.
So far we've seen how advantage changes the odds of rolling a specific number. But what about rolling greater than a specific number, as in the case of skill checks and attacks?
Here is a graph that shows the probability of rolling a specific number or greater. Shown for each number on a d20 are three probabilities: with advantage, normally, and with disadvantage.
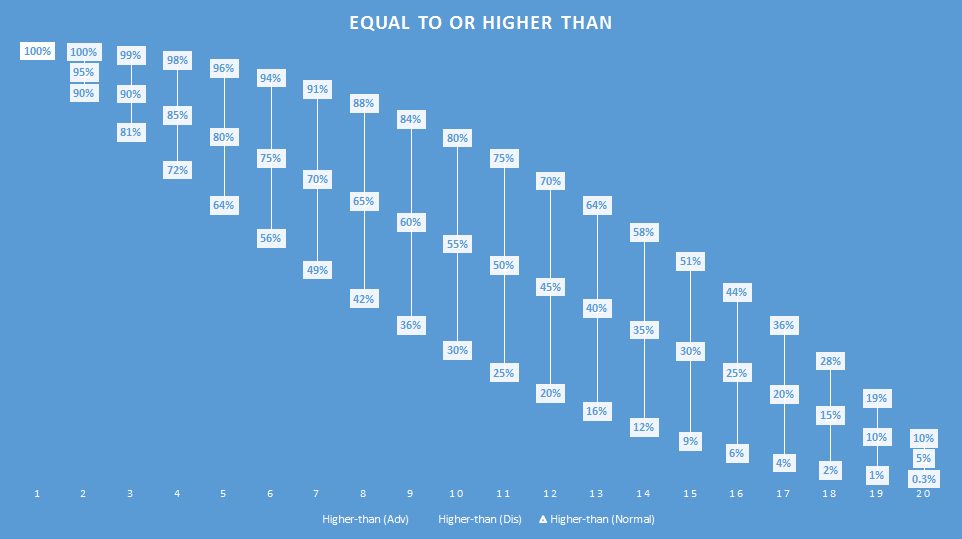
The biggest difference is rolling a 10 or greater; normally it is a 55% chance, but with advantage it swings up to 80%. With disadvantage you only have a 30% chance of rolling a 10 or greater.
Consider a level 1 character with a +2 proficiency bonus attempting to beat an Armor Class of 20. This is certainly a daunting task; under normal circumstances the chance of success is 15% (a roll of 18 or higher is needed). With disadvantage the chances are only 2%. But with advantage the chances rise to 28%, nearly double!
The natural question to ask is how does advantage compare to simple bonuses and penalties? The rules say that for passive checks,
"If the character has advantage on the check, add 5." - Player's Handbook p. 175
Does that mean having advantage is equivalent to a +5 bonus? It depends on what number you're trying to roll.
The table below shows what the bonus effectively is when you have advantage, for each number you might be trying to roll equal or higher than.
| Target Number | Bonus equivalent with Advantage | Penalty equivalent with Disadvantage |
| 1 | +0 | -0 |
| 2 | +1 | -1 |
| 3 | +2 | -2 |
| 4-5 | +3 | -3 |
| 6-7 | +4 | -4 |
| 8-14 | +5 | -5 |
| 15-16 | +4 | -4 |
| 17-18 | +3 | -3 |
| 19 | +2 | -2 |
| 20 | +1 | -1 |
Advantage is great, but disadvantage can really get a character into trouble. There are situations where you should really avoid rolling dice if you will have disadvantage. As you can see above, if you need to roll any number between 8-14 and you have disadvantage, you effectively have a -5 penalty.
I believe this places a greater emphasis on gaining advantage through creative roleplaying or superior tactics.
I'd like to think the designers of D&D 5 carefully designed this mechanic with probabilities in mind, so I will. Hopefully this brief exploration of the advantage system in D&D 5 helps you understand the probabilities involved with advantage and disadvantage, and informs your decision-making when playing.